Nhập Môn Về Phân Số
Trong toán học, việc làm việc với phân số là một phần thiết yếu mà học sinh thường gặp phải. Để thực hiện các phép toán cộng hoặc trừ các phân số, trước tiên, bạn cần phải đưa chúng về cùng một mẫu số. Điều này có nghĩa là bạn cần tìm một số chung cho tất cả các mẫu số của các phân số đó. Bài viết này sẽ giúp bạn hiểu rõ hơn về quy trình tìm kiếm mẫu số chung nhỏ nhất và các phương pháp thực hiện điều này một cách hiệu quả.
Định Nghĩa Mẫu Số Chung Nhỏ Nhất
Trước khi đi vào chi tiết, hãy cùng định nghĩa rõ ràng về khái niệm "mẫu số chung nhỏ nhất" (MSTNN). MSTNN là số nhỏ nhất mà có thể chia hết cho tất cả các mẫu số của các phân số mà bạn đang làm việc. Để tìm hiểu rõ hơn về MSTNN, hãy xem xét hai ví dụ sau đây:
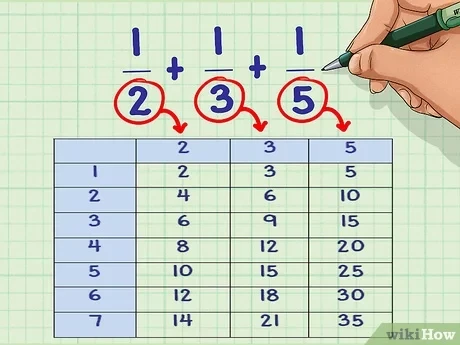
- Ví dụ 1: Nếu bạn có hai phân số 1/4 và 1/6, mẫu số chung nhỏ nhất sẽ là 12, vì 12 là số nhỏ nhất mà cả 4 và 6 đều có thể chia hết.
- Ví dụ 2: Xét hai phân số 2/3 và 3/5, mẫu số chung nhỏ nhất của chúng là 15, vì 15 là số nhỏ nhất mà cả 3 và 5 đều có thể chia hết.
Các Phương Pháp Tìm Mẫu Số Chung Nhỏ Nhất
Phương Pháp 1: Sử Dụng Bội Chung Nhỏ Nhất
Một trong những cách phổ biến nhất để tìm MSTNN là sử dụng bội chung nhỏ nhất (BCNN) của các mẫu số. Để thực hiện phương pháp này, bạn có thể làm theo các bước sau:
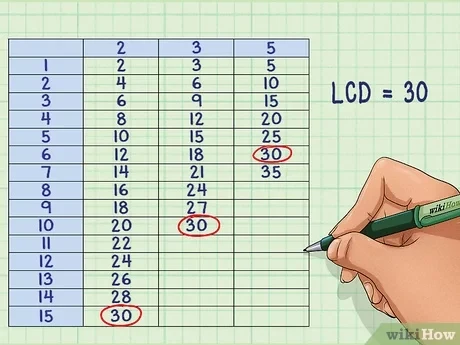
- Tìm Bội Số Chung: Liệt kê các bội số của mỗi mẫu số.
- Xác Định BCNN: Tìm bội số nhỏ nhất chung cho tất cả các mẫu số.
Ví dụ với phân số 1/8 và 1/12:
- Bội số của 8: 8, 16, 24, 32, ...
- Bội số của 12: 12, 24, 36, ...
Như vậy, MSTNN của hai phân số này là 24.
Phương Pháp 2: Phân Tích Thừa Số Nguyên Tố
Phương pháp này thường được coi là hiệu quả hơn và chính xác hơn so với việc liệt kê bội số. Để áp dụng phương pháp này, bạn thực hiện các bước sau:
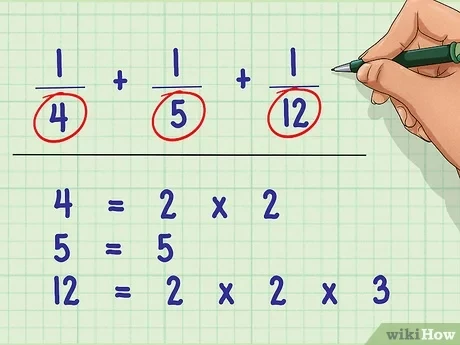
- Phân Tích Thừa Số: Phân tích từng mẫu số ra thành các thừa số nguyên tố.
- Chọn Thừa Số Chung: Chọn ra tất cả các thừa số nguyên tố, lấy số mũ lớn nhất của mỗi thừa số.
Ví dụ minh họa:
Giả sử bạn muốn tìm MSTNN cho 12 và 18.
- 12 = 2^2 × 3^1
- 18 = 2^1 × 3^2
- Thừa số 2: max(2, 1) = 2
- Thừa số 3: max(1, 2) = 2
Kết quả là MSTNN = 2^2 × 3^2 = 36.
Phương Pháp 3: Sử Dụng Quy Tắc Chia
Nếu bạn không quen với việc phân tích thừa số nguyên tố, bạn có thể sử dụng quy tắc chia. Đây là một cách thú vị và dễ nhớ hơn. Để thực hiện, bạn thực hiện theo các bước sau:
- Tìm Mẫu Số Chung: Chia sản phẩm của mẫu số đầu tiên cho mẫu số còn lại.
- Tính Toán Kết Quả: Tiếp tục cho đến khi tìm ra được mẫu số chung nhỏ nhất.
Ví dụ minh họa:
Với hai phân số 1/3 và 1/4:
- Sản phẩm của 3 và 4 là 12.
- Chia 12 cho 3, bạn có 4.
- Chia 12 cho 4, bạn có 3.
Cuối cùng, MSTNN sẽ là 12, vì 12 là mẫu số chung nhỏ nhất cho cả hai phân số.
Ứng Dụng Thực Tiễn của Mẫu Số Chung Nhỏ Nhất
Tìm được mẫu số chung nhỏ nhất không chỉ là một kỹ năng quan trọng trong việc giải quyết các bài toán phân số mà còn có các ứng dụng thực tiễn trong nhiều lĩnh vực khác nhau. Những lợi ích bao gồm:
- Giúp Giải Quyết Các Phép Tính: Khi bạn cần cộng hoặc trừ các phân số, việc tìm MSTNN giúp bạn dễ dàng thực hiện các phép toán này.
- Hỗ Trợ Trong Việc Dạy và Học Toán: Đây là một kỹ năng cần thiết trong chương trình học toán, đặc biệt là cho các học sinh ở cấp tiểu học và trung học.
- Áp Dụng Trong Các Tình Huống Thực Tế: Việc tìm MSTNN có thể được áp dụng trong các tình huống thực tế như tính toán tỷ lệ, phân chia công việc, hay bất kỳ tình huống nào cần làm việc với phân số.

Kết Luận
Tìm mẫu số chung nhỏ nhất là một kỹ năng quan trọng trong toán học mà mọi người cần nắm vững. Qua ba phương pháp chính mà chúng tôi đã trình bày, bạn có thể dễ dàng tìm ra MSTNN cho các phân số khác nhau. Việc nắm rõ quy trình và các bước cần thực hiện sẽ giúp bạn trở thành một người giải quyết vấn đề hiệu quả hơn. Hy vọng bài viết này đã cung cấp cho bạn những thông tin hữu ích và giúp bạn tự tin hơn trong việc làm việc với phân số.